
Vensim 是一款工业级仿真软件,用于提高实际系统的性能。Vensim 丰富的功能集强调模型质量、数据连接、灵活的分发和先进的算法。适合从学生到专业人士的所有人的配置。
● 高品质、尺寸一致性和 Reality Checks™
● 连接数据和复杂的校准方法
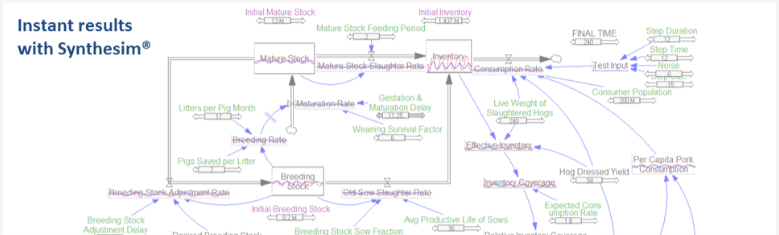
● SyntheSim 中的连续模拟即时输出
● 灵活的模型发布
● 模型分析,包括优化和蒙特卡罗模拟
● 因果追踪™
● 订阅
● 优化
● 资源分配算法
因果追踪™
订阅
优化
按优先级分配
在构建模型和分析现有模型的过程中,发现哪些事物导致其他事物发生变化非常有用。从一个方向看,您可以发现哪些变量导致特定变量发生变化。从另一个方向看,您可以发现特定变量更改(或使用)了哪些变量。所研究的变量称为“工作台变量”。

模型行为可能很难快速分析,尤其是在尝试准确发现哪些变量和反馈循环正在对特定变量贡献某些行为组成部分时。考虑下面的模型。该模型包含许多相互作用的反馈循环,这些循环会产生变量 Backlog 的振荡行为。为什么 Backlog 会出现波动?
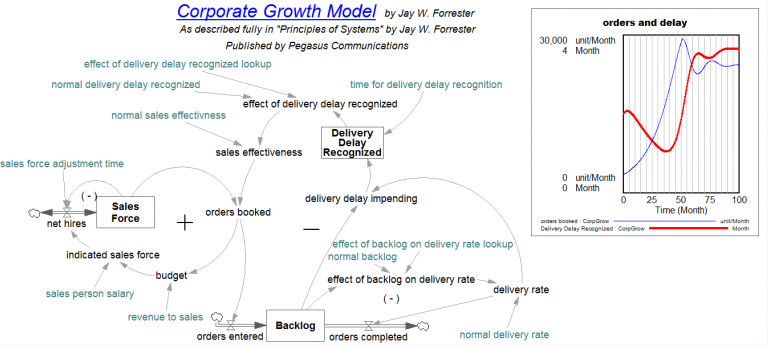
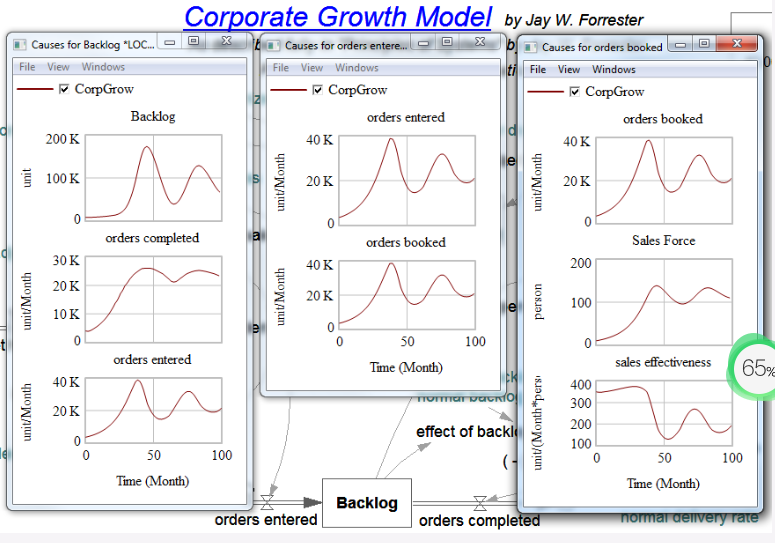
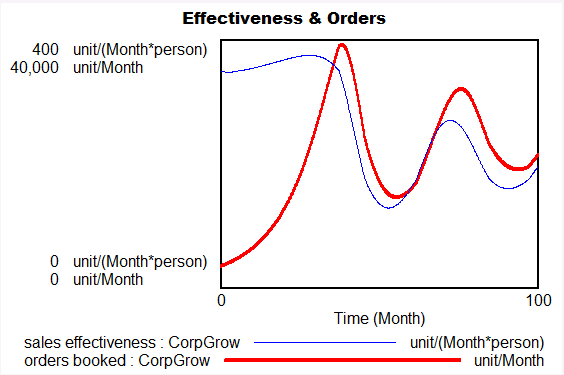
通常,一个模型结构需要一遍又一遍地重复。例如,零售店可能会在许多不同的地区复制,或者工厂的生产过程可能会重复多次。重复结构的一种方法是创建和调试一个结构,然后根据需要多次复制该结构。然而,这可能会导致复杂的图表以及恒定值和结构数量的硬连线。重复结构的更好方法是使用下标。创建下标并将其添加到一个原始结构中,从而创建与下标元素一样多的结构。现在可以轻松更改结构的数量和所有结构的数值。图表也更加整洁。
零售店(例如鞋类零售商)可能在三个地点设有商店。可以为一家商店构建一个模型,其中包含员工、库存、销售等结构。模型正确模拟后,就会创建一个名为“位置”的下标,其中下标元素为波士顿、纽约和旧金山。将下标 Location 添加到 one store 结构中,修改常量以反映每个位置的值,现在 one 模型包含三个结构。
在包含劳动力的公司中,下标 [worktype] 可能代表公司中工人的类型,下标 [location] 可能代表办公室或工厂的物理位置。所以等式


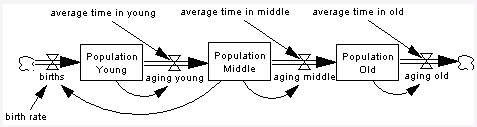
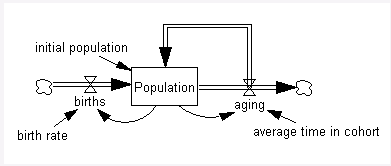
下标可以允许构建代表同一物理过程的许多不同部分的单一库存。例如,人口老龄化链由多个股票构成,其中人们老化并进入下一个股票,如下所示:
下标有几个专门用于操作方程的特殊函数。SUM 函数对标有感叹号 (!) 的下标的所有值求和。其他函数包括乘积、最大值和最小值。

模型完整性的验证部分取决于将模型行为与“现实世界”中收集的时间序列数据进行比较。当模型结构完整并且模拟正确时,可以继续模型校准以使模型适合该观察到的数据。动态模型通常对常数参数的值非常敏感。如果您想要校准参数以使模型行为与观察到的数据相匹配,您可能需要尝试数千种不同参数值的组合。Vensim 校准使此过程自动化。您指定要拟合的数据系列以及要调整的参数,然后 Vensim 会自动调整参数以获得模型行为和数据之间的最佳匹配。要调整的参数数量或要拟合的数据系列的数量没有限制。
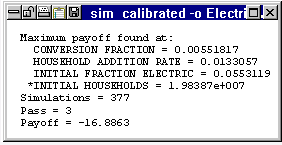
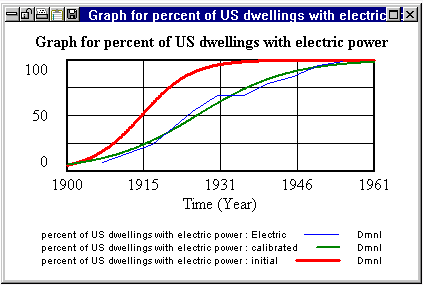
在上个世纪,美国家庭对电力的转换遵循扩散模式,以低音扩散模型为代表。一旦结构完成并产生所需的行为模式,我们就可以校准模型以适应美国商务部的历史数据。第一次模拟运行(第一次运行)显示与历史数据(历史)相比增长太早且太快。用户选择具有未知或不确定值的参数并选择历史数据系列,然后Vensim优化引擎搜索最适合数据的参数值,并显示参数值和最佳模拟运行(校准)。
Vensim 的优化引擎可以搜索大量参数值,寻找最佳解决方案。您定义要调整的收益变量。高效的鲍威尔爬山算法搜索参数空间,寻找最大的累积收益。搜索的收益变量或策略参数的数量没有限制。优化模拟可提供高级灵敏度分析。
公司必须管理库存和销售供应链才能实现公司利润最大化。库存太少会导致销售损失(并降低利润),但库存太多会增加库存成本,也会导致利润降低。用户选择收益变量(在本例中为累积利润),然后选择策略参数(开始补货的最小库存值和停止补货的最大库存值)。Vensim 优化引擎搜索给出最佳回报值(最高累积利润)的策略参数值,并打印出这些值和最佳模拟运行。
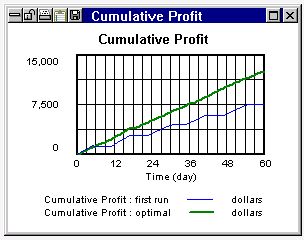
在具有不可观察变量的动态系统中,希望但不可能始终知道所有变量的状态。但是,如果某些变量的值已知,您可以很好地估计其他变量的值。例如,业务模型可能由劳动力/库存系统组成。目标是在给定可用测量的情况下确定劳动力、库存和其他模型变量的时间概况。Vensim 在卡尔曼滤波器处于活动状态时对模型进行仿真,并根据模型简单仿真数据(下图中的 simple.vdf)和测量库存数据 (data.vdf) 对输出做出智能选择。结果输出卡尔曼滤波。
有几种标准的分配建模方法,但每种公式都至少有一个重要缺陷。例如,一种方法是根据简单的公式为每个供应商分配需求的一小部分“f”:
f i = (a i / sum(a i )) * 需求
在哪里
f i = 供应商 i 赢得的需求比例(换句话说,供应商 i 的市场份额)
a i = 供应商 i 的产品的吸引力(如果价格是产品之间的唯一差异,a i 可能是 1/价格i)sum(a i ) 是所有吸引力的总和。
这个公式有许多理想的特性,但它没有受到一个限制:一个微小的供应商有可能占领整个市场。例如,假设需求是文字处理软件的全球总需求。进一步假设只有两个竞争对手:微软和 JoeBob's。微软是世界巨头;乔鲍勃的两个十几岁的兄弟(乔和鲍勃)在父母的厨房里经营。如果乔和鲍勃设法编写出比微软更好(更有吸引力)的产品(以前已经做过——记住 Intuit),那么上述公式将立即将大部分市场授予乔鲍勃。
我们可以通过两种方式解决这个问题。一种方法是在吸引力数字中纳入可见度衡量标准。在这种情况下,JoeBob 的产品可能是最好的,但由于缺乏口碑和广告,其吸引力会很小。但如果他们通过杂志上的评论而迅速获得宣传呢?为了正确地做到这一点,我们必须在吸引力中考虑乔鲍勃超负荷的电话等的影响。
正如这个例子所表明的,分配问题比看起来更棘手。
现实分配逻辑的要求
ALLOC P 函数由 William T. Wood 发明,旨在应对寻找满足所有所需属性的算法的挑战。为了确保真实性和灵活性,有五个所需的属性:
● 在任何情况下,向接收部门交付的货物总和必须等于从供应部门交付的数量。
● 所有交付(分配)必须是积极的。
● 任何行业都不应收到超过其订单的订单。
● 在供应充足的情况下,每个部门都应该准确收到其订购的产品。
● 在短缺的情况下,独特的低优先级部门应该得到很少或根本没有;如果有一个独特的高优先级行业且需求量大,那么它几乎应该获得一切,将其竞争对手拒之门外。
在市场份额双重计划中,同样的五个要求是:
● 在任何情况下,所有供应商的销售额之和必须等于总需求。
● 所有销售额和市场份额必须为正。
● 任何供应商都不能销售超过其容量的产品。
● 在需求极度过剩的情况下,每个供应商都应该出售其全部产能。
● 在需求有限的情况下,特别缺乏吸引力的供应商应该很少销售或根本不销售。如果有一个具有独特吸引力且产能高的供应商,它应该赢得几乎整个市场,将其竞争对手拒之门外。
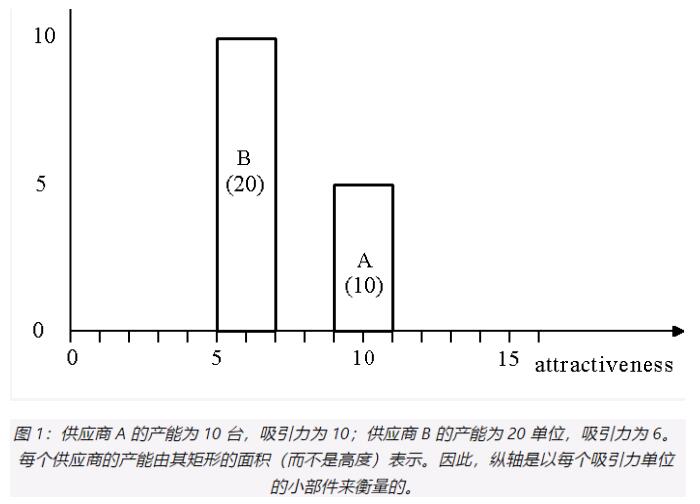
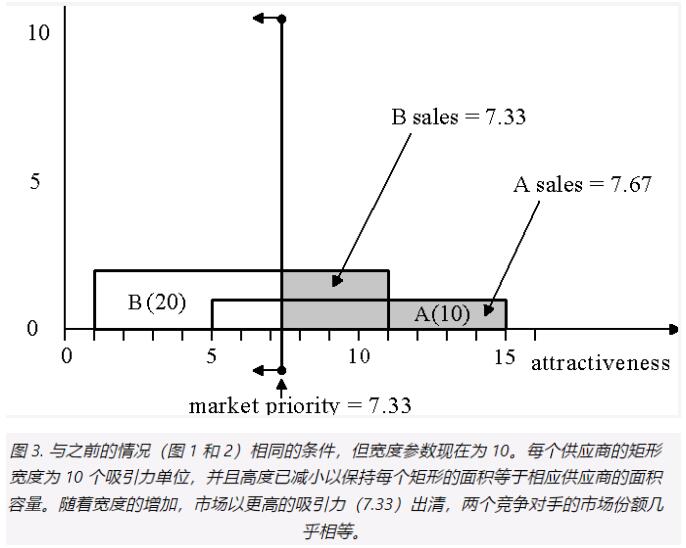
Wood 算法的灵感来自几何学,因此最好以图形方式理解它。假设有两个供应商 A 和 B,产能分别为 10 和 20 个小部件。我们用一个矩形来表示每个供应商的产能,因此该图类似于条形图,只不过每个供应商的产能是用 其矩形的面积 而不是高度来表示的。使用面积而不是高度的原因很快就会变得显而易见。
对于我们的第一个示例,我们从宽度为 2 个吸引力单位的矩形开始。正如我们所说,选择每个供应商矩形的高度以使矩形的面积等于供应商的容量。供应商 A 的容量为 10,因此其矩形的高度为 10/2,即每个吸引力单位有 5 个分配单位。供应商 B 的容量为 20,因此其高度为 10。每个供应商矩形的中心位于 X 轴上供应商产品的吸引力值处:更具吸引力的供应商(与其供应能力无关)被放置在 X 轴上。正确的。供应商 A 和 B 的吸引力分别为 10 和 6,因此它们的矩形放置在吸引力轴上,如图 1 所示。
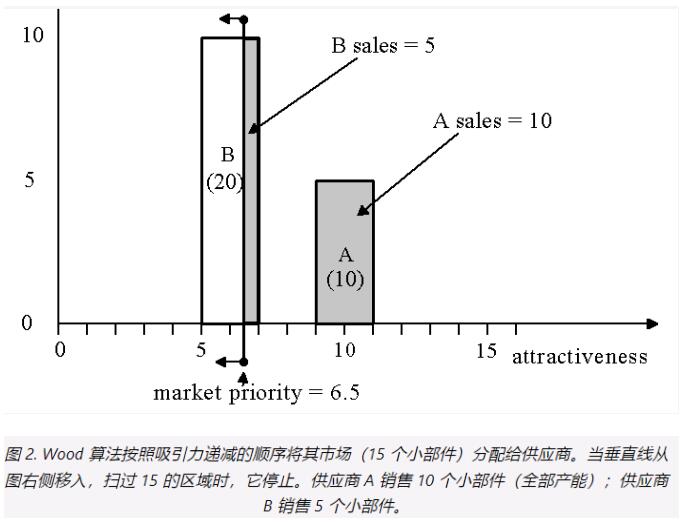
Vensim 使用 ALLOCATION BY PRIORITY 函数通过该算法分配资源。
首先,您创建一个变量(例如 mp)来保存市场优先级,然后输入 MARKETP 函数的参数:

如果变量具有多个下标,则必须使用最后进行分配的下标。例如,假设您按州将市场份额分配给不同的公司。你可能有:
